前篇很精簡的帶過了什麼是 Neural Network，他的前身、大致的架構、及不同的學習方法。有了粗略的概念之後，接下來要來介紹 Deep Learning 在做預測及訓練時的細節。

Neural Network 訓練步驟

Neural Network 說到底就是在做函數擬合，試圖找出當前問題的 f 使得 y = f(x)。拿預測男女來說，y 是男/女二元結果，x 是對於預測有利的特徵輸入， 五官輪廓, 聲音高低，等等。

—— Neural Network 為函數擬合。

一個 Neural Network 學習擬合 f 的大致步驟如下：

1. 備好 dataset，也就是好幾筆 (x, y) =（feature, label） 的 data
2. 對每一筆輸入 feature 進行prediction（預測），得到輸出
3. 計算預測結果 與正確答案 y 的 error（誤差），或稱 loss
4. 將 loss backpropogate（反向回饋） 給 network 裡的 parameters以進行修正，目標是減少下次預測的 loss

所以 Deep Learning 學習的成果，就是能準確預測結果的 model parameters。

我們將關鍵步驟分為兩大步：prediction (2.) 和 training (3. & 4.)。本篇的重點會擺在 prediction 這一步。下面會多一些數學，希望不會太難，也為深入理解 Deep Learning 內含的數學做準備。

Prediction

前篇有介紹過 Perceptron 怎麼被訓練的。由於 Neural Network 是由很多類似 Perceptron 的 Neuron 層層連結而成，大致上的步驟也與之相似。

Prediction 這步基本上就是把資訊往 network 裡送，傳到最後一層取得 output，這動作稱為 feed forward 或 forward propagation，步驟大致如下：

1. 從上層接收 input x
2. 與 weights w 透過 summation and bias 進行加權整合
3. Activation 決定該 neuron 是否被激發
4. 產出 prediction output

Input & Weights

第一層的輸入訊息是來自大環境的，例如圖片、文字、聲音等各種 feature，而接下來 hidden layer 則是接收前面幾層傳來的分析處理過的訊息來進行整合。

你會問，這些層跟層之間的訊息有什麼含意嗎？

肯定有，但只有 network 自己懂。人類想理解中途的訊息很困難，因為他是很高程度的 abstraction（抽象概念），而學者們也致力於讓這些訊息變得可理解。這也是為什麼 Neural Network 被稱為黑盒子，因為沒人懂他怎麼塞進輸入後就能產生準確預測，也不懂訓練不起來的時候原因出在哪。

讓我們往 engineering 的角度靠近一步。如果圖片、文字、聲音都能當輸入，那我們建立好的 network 要怎麼同時照顧好這麼多不同資料的形式？因此，這些輸入都要先轉化成較為統一的模樣。

Vector & Matrix 資料形式

讓我們回顧一下 summation and bias 在做什麼：

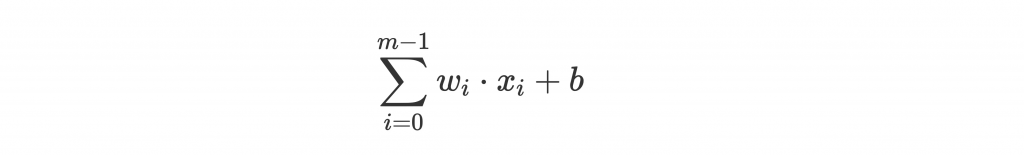
後面的 b 是 bias，前篇有提過是讓 activation 的門檻標準變得可訓練。但他在式子裡好像有點礙眼，因為跟前面 m 個 w 走在不同路上！

這時候有個小技巧：

這邊 ，。

也就是我們把 b 當成 weights 的一份子（因為 weights 和 bias 同為可訓練的 parameters），並將他對應的 x 設為 1，即可合併進入 summation。

這個技巧能讓 code 更簡單！

前面的 summation ，無論是數學上看起來或是 code 寫起來都略顯麻煩。這時候我們可以把他們轉化為 vector（向量） 來進行計算：

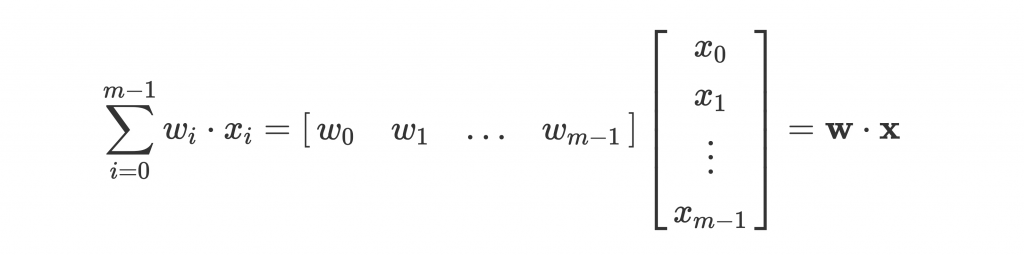
是不是簡單許多？

這是單個 neuron 的輸出，我們甚至可以用 matrix（矩陣） 來一次打包一層的 neurons。請參考下面的例子：

—— Matrix 來進行 summation。

a 是 activation 之後的結果，我們先看 summation 之後的輸出 z 可以怎麼表示：

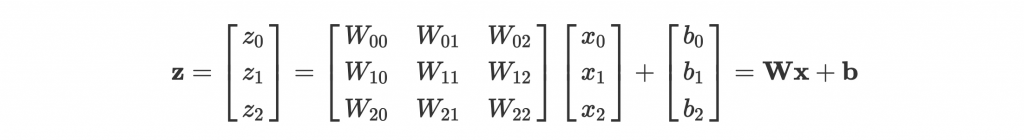
一個簡單的式子就能代表一整層的 feed forward！而利用 matrix 來運算，除了讓數學簡單一點（特別是後面會提到的 gradient descent），也能讓電腦硬體優化運算，訓練更快速。

雖然睡前可能不會想做，但有障礙的朋友記得小小複習一下 linear algebra（線性代數），對後面的數學會很有幫助的。

Input Pre-processing

回到統一輸入形式這邊。理解 summation and bias 這步基本等於 之後，應該就不難理解輸入形式應該統一為 vector ，以利電腦的運算。

也就是在整個 network 開始學習前會進行 pre-processing（前置處理），將圖片轉成 vectors of pixels，文字轉成 word vectors（這個之後會介紹到，將字詞轉化為 vector 形式），聲音轉化成 vectors of frequency 等等，才能進入 network 進行訓練。而怎麼讓轉化為 vectors 的 input 最大限度的保留原本的資訊，也是一件值得深入的話題！

Input 和 weights 整合完後，我們代稱結果為 z，i.e. 。

Activation

Activation 是根據前面處理好的訊息 z，決定激發程度。前篇 Perceptron 提到在 activation 時用 step function 進行激發與否的二元標準判斷。而在 Neural Network 裡，每個 neuron 輸出的是激發程度，也就是不只是 0 或 1，而是更細微的訊息。

在這個步驟我們計算的是上面途中的 a = g(z)，g 為 activation function。為了學習 non-linear approximation，activation function 通常是 non-linear function（非線性函數）。

除了是 non-linear function，還有些必備條件：derivative（導數）容易計算，且 derivative 適用於訓練。例如 step function 雖然是 non-linear function，但因為他的導數不適合用來訓練（兩邊導數都是 0，能提供的回饋也是 0 啊⋯⋯），並不適合被用在 hidden layer 的 activation。

微積分從腦中消逝的也麻煩找尋一下記憶。

這些條件跟之後 back propagation 需要用到的 gradient descent 有關，之後會詳細解說。

常見 Activation Functions

常用的 Activation function 很多，簡單示範幾個：

Sigmoid	Tanh	ReLU

e 沒有很可怕，e 只是個常數， 的導數為 ，很美。

值得注意的是 sigmoid 的輸出範圍介在 0 和 1 之間，呈遞增，且中間為 0.5，很適合把分數化為機率，除了用在 hidden layer 的 activation，也常用在 binary classification 的 output layer 當作預測種類的機率。

而 ReLU 看似簡單，其實經過一些實驗發現效果非常好，而且 derivative 也比 sigmoid 簡單許多，與他的變形們是近幾年的主流選擇。

這些 function 都符合的上述的條件：導數都很優雅（之後會看到他們的 derivative），且適合訓練（例如 ReLU，分數越高激發程度越高，導數能提供的訊息也很清楚）。

Softmax Function

最後再介紹一個在 multiclass classification 時，很常用在最後一層的 Softmax function。他的概念是 normalize（標準化）最後一層得到 z 的分數，使得可正可負且沒有絕對意義的分數值，變成 probability（機率） 的意義。

例如你在做貓的種類判斷，有三個種類，那麼 Softmax 出來的結果並不是 100% 波斯貓，而是 90% 機率波斯貓、5% 機率英國短毛貓、5% 機率蘇格蘭摺耳貓等等。

Softmax function 表示如下（C 為 number of classes（類別數）， 為第 i 種類別的分數）：

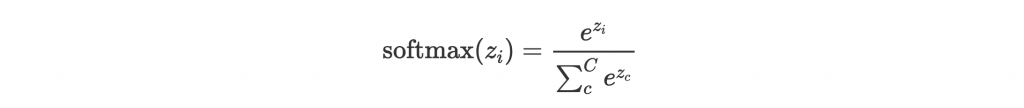
可以看到分母的 summation 就是在進行 normalization，讓每個類別的分數介於 0，1 之間，且合為 1。而這個分數就代表預測為該類別的機率。所以最後一層要有幾個 neuron 會等於要做判斷的種類數 C 喔！

Prediction

經由 pre-processing 把 network 的 input 轉化為 vector 形式後，經過一層層的處理，每層統整激發： 並把輸出傳遞下去，直到最後一層激發完後，獲得 prediction 。Prediction 這步就完成了。

而 predict 完之後，接著把 error 回饋給 network 的參數，便是下一篇的主題。

Checkpoint

• Neural Network 的終極目標為何？
• 訓練 Neural Network 的大致流程為何？
• 用 vector 和 matrix 來表示 data 有哪些好處？
• 試著從上面 matrix summation 的範例圖，標示每條線對應到 裡的值。
• Activation function 有哪些條件？
• Softmax function 常被應用在哪種任務？

參考資料

1. Wikipedia - Activation Function
2. CS224n Lecture Notes Part III - Neural Networks, Backpropagation
3. CS224n Lecture 3 Slides - Word Window Classification, Neural Networks, and PyTorch
4. ? CS229 Lecture Notes - Deep Learning

延伸閱讀

1. CS229 Lecture Notes - Linear Algebra Review and Reference